Top 5 Sorting Algorithms Compared
Compare and implement Bubble Sort, Selection Sort, Insertion Sort, Merge Sort, and Quick Sort. Learn their time complexities and use cases.
Sorting algorithms are fundamental to computer science and play a crucial role in optimizing the performance of various applications. Whether you're organizing a list of names or managing complex dataset, understanding how to efficiently sort data is essential. In this article, we'll delve into five popular sorting algorithms: Bubble Sort, Selection Sort, Insertion Sort, Merge Sort, and Quick Sort. We'll explore how each algorithm works, their time complexities, and practical use cases to help you choose the right one for your needs. By the end of this guide, you'll have a solid grasp of these sorting techniques and be better equipped to handle sorting challenges in your projects. Let's get started!
Introduction to Sorting Algorithms
Sorting is a critical operation is computer science, affecting everything from basic data management to complex algorithms in machine learning and database optimization. Different sorting algorithms offer unique advantages and trade-offs, making it important to understand their inner workings and applications.
Overview of Algorithms Covered
In this article, we'll explore the following sorting algorithms:
Bubble Sort
Selection Sort
Insertion Sort
Merge Sort
Quick Sort
Each of these algorithms has its own strengths and weaknesses, and we'll discuss when to use each one. Now, let's dive into the first algorithm on our list: Bubble Sort.
Bubble Sort
Bubble Sort is one of the simplest sorting algorithms to understand and implement. It works by repeatedly stepping through the list, comparing adjacent elements and swapping them if they are in the wrong order. This process continues until the list is sorted. Here's a more detailed look at how Bubble Sort operates:
How Bubble Sort Works:
Start at the beginning of the list.
Compare the first two elements. If the first element is greater than the second, swap them.
Move to the next pair of elements and repeat the comparison and swap if necessary.
Continue this process until the end of the list is reached.
Repeat the entire process for the remaining elements, ignoring the last sorted element each time.
The algorithm terminates when no swaps are needed during a complete pass through the list.
Time Complexity:
Best Case: O(n)
Average Case: O(n^2)
Worst Case: O(n^2)
Practical Use Cases:
Bubble Sort is not suitable for large datasets due to its inefficiency, but it can be useful for educational purposes and small lists where simplicity is more important than performance.
Example Implementation:
# Python
def bubble_sort(array):
for i in range(len(array)):
for j in range(len(array) - i - 1):
if array[j] > array[j + 1]:
array[j], array[j + 1] = array[j + 1], array[j]
return array
arr = [5, 3, 8, 4, 6]
print(bubble_sort(arr))
// JavaScript
function bubbleSort(array) {
let swapped;
do {
swapped = false;
for (let i = 0; i < array.length; i++) {
if (array[i] && array[i + 1] && array[i] > array[i + 1]) {
[array[i], array[i + 1]] = [array[i + 1], array[i]];
swapped = true;
}
}
} while (swapped);
return array;
}
const arr = [5, 3, 8, 4, 6];
console.log(bubbleSort(arr.slice()));
Selection Sort
Selection Sort is another simple sorting algorithm, but it typically performs better than Bubble Sort. It works by repeatedly finding the minimum element from the unsorted portion of the list and moving it to the beginning. Here's a closer look at how Selection Sort operates:
How Selection Sort Works:
Start with the first element as the current minimum.
Compare this minimum with the remaining elements to find the actual minimum element in the unsorted portion.
Swap the found minimum element with the first element.
Move to the next element and repeat the process until the entire list is sorted.
Time Complexity:
Best Case: O(n^2)
Average Case: O(n^2)
Worst Case: O(n^2)
Practical Use Cases:
Selection Sort is also not suitable for large datasets due to its O(n^2) time complexity. However, it is easy to understand and implement, making it useful for educational purpose and small lists where performance is not critical.
Example Implementation:
// Java
public class SelectionSort {
public static void main(String[] args) {
int[] arr = {4, 2, 6, 9, 11};
int[] res = selectionSort(arr);
System.out.println("Sorted array: ");
printArray(res);
}
private static int[] selectionSort(int[] array) {
for (int i = 0; i < array.length; i++) {
int minIndex = i;
for (int j = i + 1; j < array.length; j++) {
if (array[j] < array[minIndex]) {
minIndex = j;
}
}
swap(array, i, minIndex);
}
return array;
}
private static void swap(int[] array, int i, int j) {
int temp = array[i];
array[i] = array[j];
array[j] = temp;
}
private static void printArray(int[] array) {
for (int element : array) {
System.out.print(element + " ");
}
System.out.println();
}
}
# Python
def selection_sort(array):
for i in range(len(array)):
min_index = i
for j in range(i + 1, len(array)):
if array[j] < array[min_index]:
min_index = j
array[i], array[min_index] = array[min_index], array[i]
return array
arr = [5, 3, 8, 4, 6]
print(selection_sort(arr))
Key Points to Remember
Selection Sort repeatedly selects the smallest (or largest, depending on sorting order) element from the unsorted portion and moves it to the sorted portion.
Despite its inefficiency for large lists, it is conceptually straightforward and provides a good introduction to sorting algorithms.
Insertion Sort
Insertion Sort is an efficient algorithm for sorting small datasets or partially sorted lists. It works similarly to how people sort playing cards in their hands: by taking one card at a time and inserting it into the correct position relative to the already sorted cards. Here's a closer look at how Insertion Sort operates:
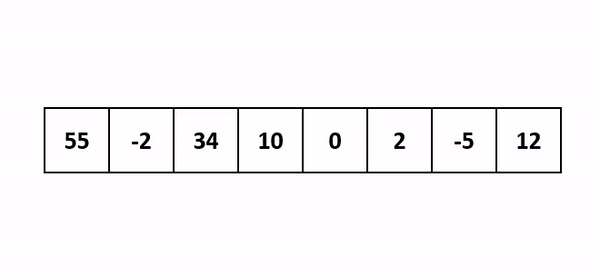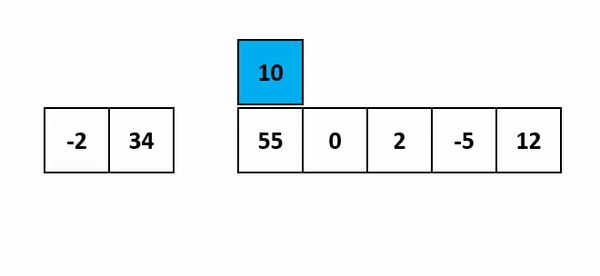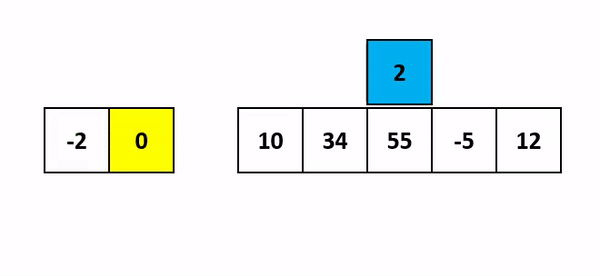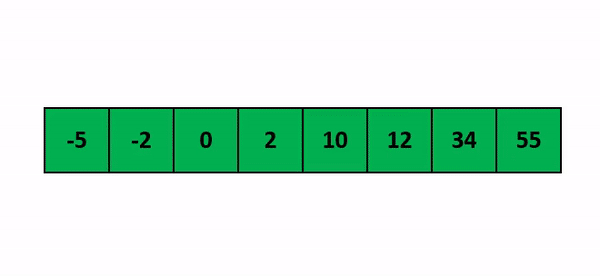
How Insertion Sort Works:
Start with the second element (the first element is considered sorted).
Compare the current element with the elements in the sorted portion of the list.
Shift the sorted elements to the right until the correct position for the current element is found.
Insert the current element into its correct position.
Repeat the process for each element until the entire list is sorted.
Time Complexity:
Best Case: O(n)
Average Case: O(n^2)
Worst Case: O(n^2)
Practical Use Cases:
Insertion Sort is particularly useful for small datasets or lists that are nearly sorted, as it can be more efficient than more complex algorithms in these cases. It's also a stable sorting algorithm, meaning it maintains the relative order of equal elements.
Example Implementation:
// C++
#include <iostream>
using namespace std;
void insertionSort(int array[], int n) {
for (int i = 1; i < n; i++) {
int key = array[i];
int j = i - 1;
while (j >= 0 && array[j] > key) {
array[j + 1] = array[j];
j--;
}
array[j + 1] = key;
}
}
void printArray(int array[], int n) {
for (int i = 0; i < n; i++) {
cout << array[i] << " ";
}
cout << endl;
}
int main() {
int arr[] = {23, 1, 10, 5, 2};
int n = sizeof(arr) / sizeof(arr[0]);
insertionSort(arr, n);
cout << "Sorted array: ";
printArray(arr, n);
return 0;
}
# Python
def insertion_sort(array):
for i in range(1, len(array)):
key = array[i]
j = i - 1
while j >= 0 and array[j] > key:
array[j + 1] = array[j]
j -= 1
array[j + 1] = key
return array
arr = [23, 1, 10, 5, 2]
print(insertion_sort(arr))
Key Points to Remember
Insertion Sort builds the sorted array one item at a time, inserting each new item into its proper place among the previously sorted items.
It is adaptive, meaning it is efficient for datasets that are already substantially sorted: the time complexity is O(n) when each element is no more than a constant number of positions away from its final position.
Merge Sort
Merge Sort is a highly efficient, comparison-based sorting algorithm that uses the divide-and-conquer approach. It is well-suited for sorting large datasets and is known for its stability and consistent performance. Here's a closer look at how Merge Sort operates:
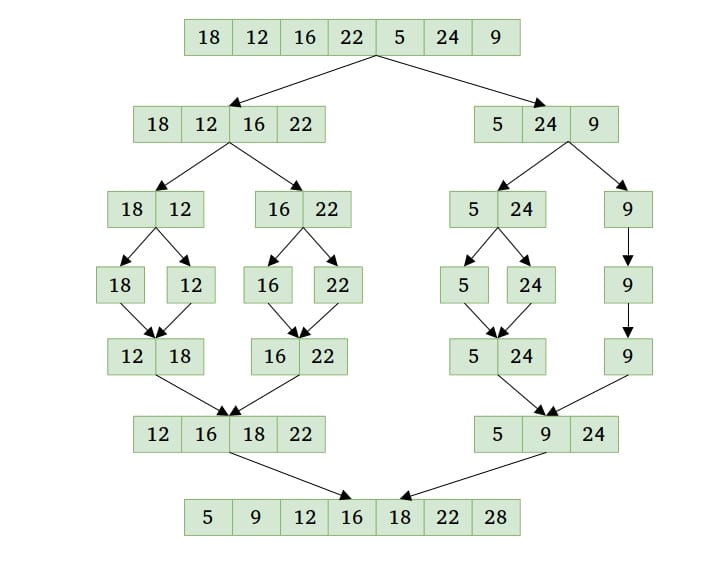
How Merge Sort Works:
Divide: Split the unsorted list into two approximately equal halves.
Conquer: Recursively sort each half.
Combine: Merge the two sorted halves back together into a single sorted list.
The merging process involves comparing the smallest elements of each half and repeatedly moving the smaller element to the new sorted list until all elements from both halves are exhausted.
Time Complexity:
Best Case: O(n log n)
Average Case: O(n log n)
Worst Case: O(n log n)
Practical Use Cases:
Merge Sort is particularly effective for large datasets and for data stored in external storage. It is also useful when the data cannot be loaded entirely into memory (external sorting). Additionally, Merge Sort is stable, preserving the relative order of equal elements.
Example Implementation:
// Java
public class MergeSort {
public static void main(String[] args) {
int[] arr = {24, 2, 12, 92, 34};
int[] res = mergeSort(arr);
System.out.println("Sorted array: ");
printArray(res);
}
private static int[] mergeSort(int[] array) {
if (array.length <= 1) {
return array;
}
int mid = array.length / 2;
int[] left = new int[mid];
int[] right = new int[array.length - mid];
System.arraycopy(array, 0, left, 0, mid);
System.arraycopy(array, mid, right, 0, array.length - mid);
left = mergeSort(left);
right = mergeSort(right);
return merge(left, right);
}
private static int[] merge(int[] left, int[] right) {
int[] result = new int[left.length + right.length];
int i = 0, j = 0, k = 0;
while (i < left.length && j < right.length) {
if (left[i] <= right[j]) {
result[k++] = left[i++];
} else {
result[k++] = right[j++];
}
}
while (i < left.length) {
result[k++] = left[i++];
}
while (j < right.length) {
result[k++] = right[j++];
}
return result;
}
private static void printArray(int[] array) {
for (int element : array) {
System.out.print(element + " ");
}
System.out.println();
}
}
# Python
def merge_sort(array):
if len(array) <= 1:
return array
mid = len(array) // 2
left = merge_sort(array[:mid])
right = merge_sort(array[mid:])
return merge(left, right)
def merge(left, right):
result = []
i, j = 0, 0
while i < len(left) and j < len(right):
if left[i] <= right[j]:
result.append(left[i])
i += 1
else:
result.append(right[j])
j += 1
result += left[i:]
result += right[j:]
return result
arr = [5, 2, 4, 1, 3]
print(merge_sort(arr))
Key Point to Remember
Merge Sort is an efficient, stable, and consistent sorting algorithm with a time complexity of O(n log n) for all cases.
It uses the divide-and-conquer approach to split the list into smaller sublists, sort each sublist, and then merge the sorted sublists back together.
Merge Sort is well-suited for large datasets and external sorting where the data cannot fit into memory.
Quick Sort
Quick Sort is a highly efficient sorting algorithm known for its speed and widespread use in various programming languages and libraries. It follows the divide-and-conquer approach, similar to Merge Sort, but typically performs better in practice for most datasets. Here’s a closer look at how Quick Sort operates:
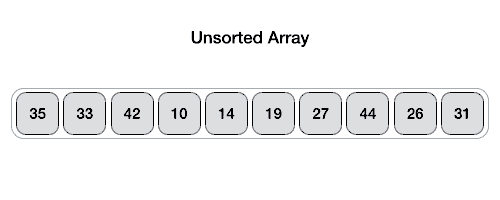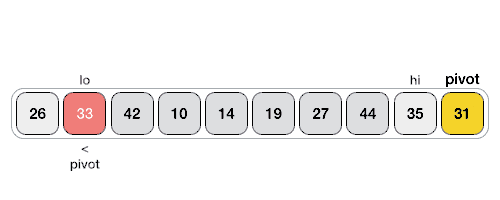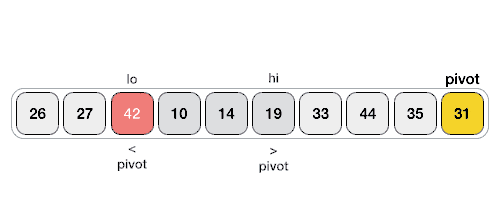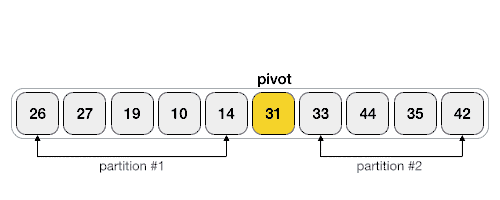
How Quick Sort Works:
Partitioning: Choose a pivot element from the array and partition the array into two subarrays: elements less than the pivot and elements greater than the pivot.
Recursion: Recursively apply the same process to the subarrays.
Combine: No explicit merging step is needed, as the array is sorted in place during the partitioning step.
Time Complexity:
Best Case: O(n log n)
Average Case: O(n log n)
Worst Case: O(n^2) [rare, occurs when the pivot selection is poor]
Practical Use Cases:
Quick Sort is widely used in practice due to its efficiency and versatility. It performs well on average and is often faster than other sorting algorithms, especially for large datasets. However, it may perform poorly on already sorted or nearly sorted lists, as well as on datasets with many duplicate elements.
Example Implementation:
# Python
def quick_sort(array):
if len(array) <= 1:
return array
else:
pivot = array[len(array) // 2]
left = [x for x in array if x < pivot]
middle = [x for x in array if x == pivot]
right = [x for x in array if x > pivot]
return quick_sort(left) + middle + quick_sort(right)
arr = [3, 6, 8, 10, 1, 2, 1]
print(quick_sort(arr))
// JavaScript
function quickSort(array) {
if (array.length <= 1) {
return array;
}
const pivot = selectPivot(array);
const left = [];
const middle = [];
const right = [];
for (let element of array) {
if (element < pivot) {
left.push(element);
} else if (element > pivot) {
right.push(element);
} else {
middle.push(element);
}
}
return [...quickSort(left), ...middle, ...quickSort(right)];
}
function selectPivot(array) {
return array[Math.floor(array.length / 2)];
}
const arr = [3, 6, 8, 10, 1, 2, 1];
console.log(quickSort(arr));
Key Points to Remember
Quick Sort is an efficient, in-place sorting algorithm with a time complexity of O(n log n) on average.
It works by selecting a pivot element, partitioning the array around the pivot, and recursively sorting the subarrays.
Quick Sort is often preferred for its speed and simplicity, but it may exhibit poor performance on certain datasets.
Conclusion
In this comprehensive guide, we've explored five fundamental sorting algorithms: Bubble Sort, Selection Sort, Insertion Sort, Merge Sort, and Quick Sort. Each algorithm offers a unique approach to sorting data, with its own advantages and limitations.
Bubble Sort and Selection Sort are simple but inefficient for large datasets, making them suitable primarily for educational purposes or small lists.
Insertion Sort is efficient for small datasets or partially sorted lists, as it builds the sorted array one element at a time.
Merge Sort and Quick Sort are highly efficient algorithms suitable for sorting large datasets. While Merge Sort guarantees O(n log n) time complexity for all cases, Quick Sort is often faster in practice due to its lower overhead.
When choosing the right sorting algorithm for your application, consider factors such as the size of the dataset, its initial state (sorted or unsorted), and the specific requirements of your project. Understanding the strengths and weaknesses of each algorithm will empower you to make informed decisions and optimize the performance of your code.
By mastering these sorting algorithms, you've gained valuable insights into the core principles of computer science and algorithm design. Whether you're a beginner exploring the basics or an experienced developer seeking to optimize your code, the knowledge gained from studying sorting algorithms is invaluable in your journey as a programmer.
Keep experimenting, learning, and refining your skills. Happy coding!

